ポートフォリオ運用

リターン、リスク、相関係数の中でいちばん信頼できるのは「リスクの大きさ」です　その１）

2021年7月9日

こんにちは。
投資信託クリニックの カン・チュンド です。

今、あなたの目の前に、

〇 日本株式
〇 先進国株式
〇 先進国債券 という、

『３つの置物』（投資対象）が置いてあるとしましょう。

 

これらを組み合わせて、
あなたは「いっちょ、ポートフォリオでも作るか！」
という気持ちになりました。

あなたは『３つの置物』（投資対象）のウラ側を見て、

それぞれの、

 

 

をチェックしたくなりませんか？

 

どうして、このような「かしこまったこと」をしたくなるのか？

それは、今日の『分散投資』の核となる理屈を、
私たちが無意識に受け継いでいるからです。

 

 

ズバリ申し上げましょう。

 

 

 

ハリーさんが1952年に発表した論文が、『モダンポートフォリオ理論』のはじまりであるといわれています。

「何なの、その理論って？」

そんなに堅苦しく考える必要はありません。

 

『モダンポートフォリオ理論』とは
昔からある投資の知恵を、理論的に整理整頓し直したものなのです。

いわく、

 

 

という『メッセージ』が同理論には込められています。

 

 

ちょっと整理しておきましょう。

 

 

 

 

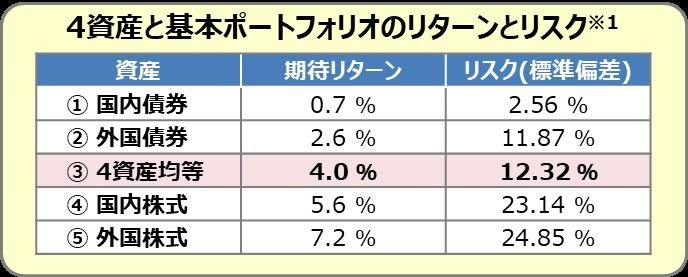
画像元：マイナビニュース

 

上記では、日本株式、外国株式（先進国株式）、
外国債券（先進国債券）とも、きちんとリターンとリスクが「数値化」されています。

（『期待リターン』の意味合いについては次述しますね。）

 

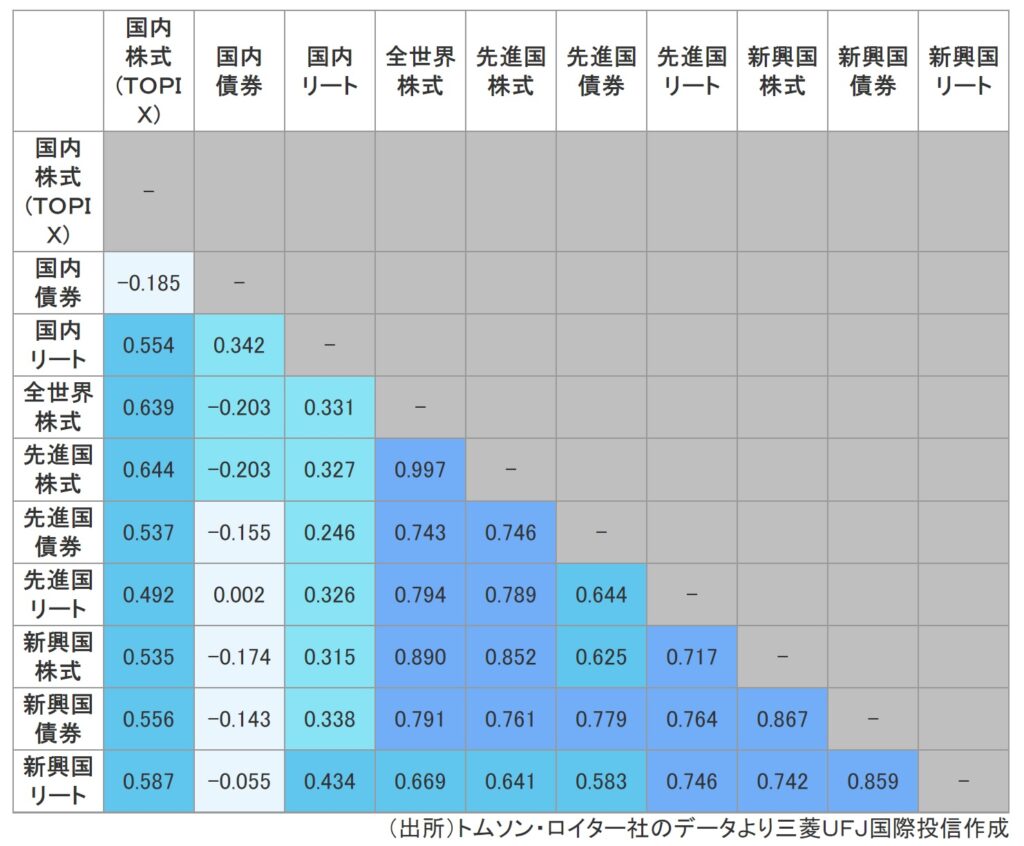
画像元：三菱UFJ国際投信

 

上記は『相関係数』の数字ですが、これは異なる投資対象間で、どの程度「値動き」が似通ってきたか、あるいは違ってきたかを「数値化」したものです。

 

 

 

以下、仮のお話ですが、

リターン、リスク（標準偏差）
関係性（相関係数）のすべてにおいて、

【過去に起きたことが、
そのまま未来にも起こる】ものなら、

私たちはかなり正確に、
ポートフォリオ（資産の組み合わせ）の
リスクとリターンの『最適ポイント』（最適配分）を導けるはずです・・。

 

 

が、残念ながら、
世の中、そう甘くはないのです。

 

実はわたしはFPになって間もない頃に、
山崎元さんの
【年金運用の実際知識】という書籍を購入しました。

 

（なんと初版は1997年！）

 

同書の中に、
次のような文章があります。

 

過去のデータを用いることについては、
W.Sharpeが
うまくまとめた表現が印象に残っています。

 

彼は、アセットアロケーションを行う場合に
過去のデータ（histric data）は、

 

標準偏差に関しては
「非常に有用」（quite useful）で

 

相関係数に関しては「そこそこに有用」
（reasonably useful）だが、

 

期待リターンに関しては
「ほとんど役に立たない」
（virtually useless）と書いており、

 

この文章を、
わたしは繰り返し繰り返し暗唱してきました。

 

 

上記はまさに
あなたが資産の組み合わせ（ポートフォリオ）を創る際、

 

 

見事に、リスクとリターンと相関係数の『特徴』を喝破しているのです。

続く・・）

カテゴリ：ポートフォリオ運用